算法复杂度
时间复杂度:指执行算法所需要的工作量。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,即考察输入值大小趋近无穷时的情况。
空间复杂度:指执行算法需要的内存空间
数据结构
栈(Stack):
后进先出的数据结构。只能在栈顶进行添加(入栈)和删除(出栈)的操作。
1 | //基本方法 |
应用:①撤销操作,②数组反转,③递归
队列(Queue):
先进先出的数据结构,只能在队尾添加(入队)元素,队首删除(出队)元素。(双向队列无尾首区别)
循环队列 性能最好
应用:排队
queue
1
2
3
4push();
pop();
front();
back();
集合(Set):
包含不重复元素的集合称为set,例如HashSet等,能快速的进行去重操作。
应用:词汇量统计
映射(Reflection):
特殊集合,例如Dictionary,存储的是键值对
应用:词汇量统计
有序数组:

- Rank使用二分查找找到target的对应位置,方便add 和 remove 的操作,保证数组始终有序
树:
二叉树(Binary Tree):普通二叉树
满二叉树(Full Binary Tree):除了叶子节点外都有两个节点
完全二叉树(Complete Binary Tree):每层的节点均达到最大值,及每层的节点数为2的n-1次方个
二叉搜索树(Binary Search Tree):每个节点左边所有节点的值均小于右边节点的值
平衡二叉树(AVL Tree):任何节点的两颗字数的高度差小于等于1
B树(B-Tree):B树与平衡二叉树一样,但是是多叉树
红黑树(Red-Black Tree):自平衡二叉寻找数
string
- substr(int pos, int len); 获得字串,pos为起始位置,len为长度
算法
排序:升序为例
冒泡:双重循环,依次比较大小,前一个比后一个大,则交换位置,时间复杂度O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13vector<int> MySort(vector<int>& arr) {
int n = arr.size();
for(int i = 0; i < n; i++){
for(int j = 0; j < n - 1; j++){
if(arr[j] > arr[j + 1]){
int t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
}
}
}
return arr;
}
选择:双重循环,但内循环只选出第 i 个即其之后位置的最小值,然后和第 i 个位置交换,时间复杂度O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17vector<int> MySort(vector<int>& arr) {
int n = arr.size(), idx = 0;
for(int i = 0; i < n; i++){
int mx = arr[i];
idx = i;
for(int j = i + 1; j < n; j++){
if(mx > arr[j]){
mx = arr[j];
idx = j;
}
}
int t = arr[i];
arr[i] = mx;
arr[idx] = t;
}
return arr;
}
快排:以第一个数为界 记flag,从前往后找出第一个比flag大的值,从后往前,找出第一个比flag小的数,然后交换两个数的位置。直到找到flag的位置,然后递归查找flag的左侧和右侧的中间值
时间复杂度O(n log2 n)
不能对存在重复元素的数组进行排序 若快排前数组有序,则时间复杂度为O(n^2) 排序前可以将第一个元素与中间或随机元素进行交换,可优化时间复杂度1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32void QuickSort(vector<int>& arr, int start, int end){
if(start >= end){
return;
}
int flag = arr[start];
int i = start, j = end;
while(true){
while(arr[++i] < flag){
if(i == end)
break;
}
while(arr[j] > flag){
j--;
if(j == start)
break;
}
if(i >= j)
break;
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
arr[start] = arr[j];
arr[j] = flag;
QuickSort(arr, start, j - 1);
QuickSort(arr, j + 1, end);
}
vector<int> MySort(vector<int>& arr) {
QuickSort(arr, 0, arr.size() - 1);
return arr;
}三路快排:有重复元素的快速排序 ,即相比上一个方法,多了等于flag的情况
即将数组中的元素分为三个区域,大于[gt, right] 小于[l+1, lt]和等于选定值flag的情况
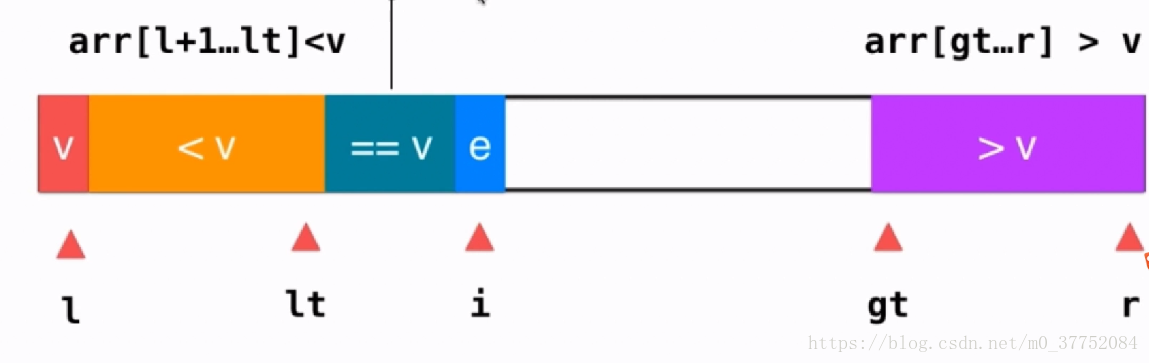
i 指向当前元素
- 若 i 指向元素等于flag,则i++;
- 若 i 指向元素小于flag,则将 it + 1 指向的值与 i 交换,然后 it++、i++。即将小于flag的区域增1,且等于flag的区域右移1.
- 若 i 指向的元素大于flag, 则将 gt - 1 指向的元素与 i 交换,然后 gt—。即将大于flag的区域向后增1,其余区域不变
- 当 i 指向 gt 时,表示遍历完成,此时只需将 flag 除的值与 lt 处的值进行交换,则三个区间形成,然后继续遍历大于flag和小于flag的区域
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33void QuickSort(vector<int> &arr, int start, int end)
{
int flag = res[start];
int i = start + 1;
int lt = start, gt = end + 1;
while(i < gt){
if(arr[i] < flag){
int t = arr[i];
arr[i] = arr[lt + 1];
arr[lt + 1] = t;
lt++;
i++;
}
else if(arr[i] > flag){
int t = arr[i];
arr[i] = arr[gt - 1];
arr[gt - 1] = t;
gt--;
}
else{
i++;
}
}
arr[start] = arr[lt];
arr[lt] = flag;
QuickSort(arr, start, lt - 1);
QuickSort(arr, gt, end);
}
vector<int> MySort(vector<int>& arr) {
QuickSort(arr, 0, arr.size() - 1);
return arr;
}
归并:采用分治法,先使子序列有序,然后将两个有序子序列合并,得到有序序列。即先将输入序列分成n/2个子序列,对这两个子序列分别采用归并排序,将两个排序好的子序列合并成排序序列,时间复杂度O(nlogn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40void Merge(vector<int>& arr, vector<int>& res, int start, int mid, int end){
int i = start, j = mid + 1, k = start;
while(i <= mid && j <= end){
if(arr[i] > arr[j]){
res[k++] = arr[j++];
}else{
res[k++] = arr[i++];
}
}
while(i <= mid){
res[k++] = arr[i++];
}
while(j <= end){
res[k++] = arr[j++];
}
for (int z = start; z <= end; z++){
arr[z] = res[z];
}
}
void MergeSort(vector<int>& arr, vector<int>& res, int start, int end){
if(start >= end)
return;
int mid = (end + start) / 2;
MergeSort(arr, res, start, mid);
MergeSort(arr, res, mid + 1, end);
Merge(arr, res, start, mid, end);
}
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
if(n <= 1){
return arr;
}
vector<int> res(n);
MergeSort(arr, res, 0, n - 1);
return res;
}
堆:
桶:
查找:
顺序查找O(n):遍历所有数据,进行处理
1
2
3
4
5
6
7
8
9
10public int OrderSearch(int[] arr, int target)
{
int n = arr.length;
for(int i = 0; i < n, i++)
{
if(target == arr[i])
return i;
}
return -1;
}二分查找O(log n):对有序数组进行分半查找,每次为对比中间数据,然后根据大小关系,对前半部分或后半部分进行对比。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public int BinarySearch(int[] arr, int target)
{
int l = 0, r = arr.length - 1, mid;
while(l <= r)
{
mid = l + (r - l) / 2; //防止数据溢出
if(target < arr[mid])
r = mid - 1;
else if(target > arr[mid])
l = mid + 1;
else
return mid
}
return -1;
}
递归(recursion):
- 程序调用自身的编程技巧称为递归,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解.。递归需要有边界条件、递归前进段和递归返回段。
- 尾递归:首先执行计算,然后执行递归调用
- 在尾部调用的是函数自身 (Self-called);
- 可通过优化,使得计算仅占用常量栈空间 (Stack Space)。
并查集
定义:在一些有N个元素的集合应用问题中,通常在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
主要用于解决一些元素分组的问题,用于管理一系列不相交的集合并存在两种操作:
- 查找(Find):查询两个元素是否在同一个集合中;
- 合并(Union):把两个不相交的集合合并成一个集合。
最简单版本的并查集代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21int parent[MaxSize]; //使用parents数组来记录每个节点的父节点
//初始化:首先将所有的节点的父节点设置为自己
void init(int n)
{
for(int i = 1; i <= n; i++)
parent[i] = i;
}
//查询:通过递归不断访问父节点,直到访问到根节点。根据两个节点的根节点是否相同来判断是否在同一个集合当中
int Find(int val)
{
if(parent[val] == val)
return x;
return Find(parent[val]);
}
//合并:找到两个节点所在集合的根节点,将一个根节点的父节点设置为另一个根节点
void Union(int i, int j)
{
parent[Find(i)] == Find(j);
}直接合并可能会导致每次查询的路径过长,而增加时间消耗,因此,存在两个方面对算法进行优化
路径压缩:在查询过程中把沿途的每个节点的父节点全部设置为根节点
1
2
3
4
5
6
7
8
9
10
11
12
13//路径压缩
int Find(int val)
{
if(parent[val] == val)
return val;
parent[val] = Find(Parent[val]); //将父节点设置为根节点
return parent[val] //返回父节点
}
//通常简化为
int Find(int val)
{
return parent[val] == val ? val:(parent[val] = Find(parent[val]);
}按秩合并:用rank[]数组记录每个根节点对应的深度。初始化为1。合并时把rank较小的合并在较大的根节点上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20void init()
{
for(int i = 1; i <= n; i++)
{
parent[i] = i;
rank[i] = 1;
}
}
void Union(int i, int j)
{
int x = Find(i);
int y = Find(j);
if(rank[x] > rank[y])
parent[y] = x;
else
parent[x] = y;
if(rank[x] == rank[y] && x != y) //如果深度相同且不是同一个根节点,则新的根节点深度加一
rank[y]++;
}
路径压缩和按秩合并如果一起使用,时间复杂度接近
,但是很可能会破坏rank的准确性。
背包问题
背包问题大体的解题模板是两层循环,分别遍历物品nums和背包容量target,然后写转移方程,根据背包的分类我们确定物品和容量遍历的先后顺序,根据问题的分类我们确定状态转移方程的写法。
01背包:外循环nums,内循环target,target倒序且target>=nums[i];
完全背包
- 组合问题:外循环nums,内循环target,target正序且target>=nums[i]
- 排列问题:外循环target,内循环nums,target正序且target>=nums[i]
分组背包:需要多重循环:外循环nums,内部循环根据题目的要求构建多重背包循环
A*算法
概述
- A*算法是一个搜索算法,是对于广搜(BFS)的优化。
- A算法类似于Dijkstra算法。不同点在于A\算法的查找优先向最可能到达终点的方向进行查找。即相较于BFS,少搜索了一些不太可能达到终点的点。
- 因为H是对未来路径的预测,所以A*算法找到的路径不一定是最短的,但牺牲准确度带来的是效率的提升
关键
- 启发函数:计算组成路径的方格的关键是以下等式
- F = G + H
- G:从起点移动到当前点的代价。
- H:从当前点移动到终点的预估代价。
- F:当前选择路径的可能总代价,作为下一个将遍历点的依据
- 对于网格形式的图,H有几种方式:
- 中能上下左右移动的,使用曼哈顿距离(|x1 - x2| + |y1 - y2|)
- 允许八个方向的,则使用对角距离
- 允许任意方向的,使用欧几里得距离(两点间的先线段长度)
为了方便观察使用和Debug,进行了一些可视化处理

算法思路
1 | private void FindPath() |
- 每帧执行
- Point类为地图中的一个点
- 将将要被遍历的点放入openList中,每次执行FindPath都会对openList中F值最小的点进行遍历,然后将其加入closeList中。
- 当openList中存在终点时,代表已经遍历至终点,从终点依次遍历其Parent点便可以得到最终路径
执行
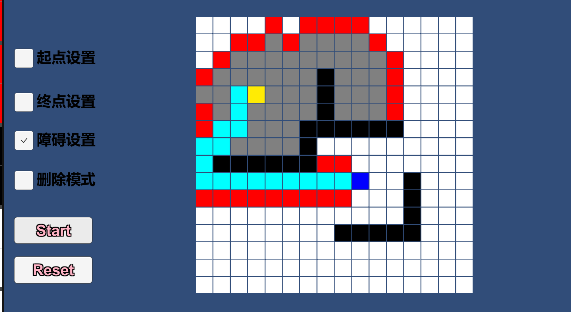
STL(C++)
- 增删查:insert()、erase()、find()
vector
初始化
1
2
3
4
5
6
7
8vector<int> vec;
vector<vector<string>> vec;
vector<int> vec2(vec);
vector<int> vec2 = vec;
vector<int> vec2{a, b, c};
vector<int> vec2(len, val);增
1
2
3vector<int> v;
v.push_back(i);
v.insert(v.begin() + idx, val);删
1
2
3
4
5
6v.pop_back(); //尾部删除
v.erase(v.begin() + idx);
//删除一段区间内的元素
v.erase(v.begin() + idx, v.begin() + idx + length);
v.clear();
set
find(T val); 返回指向对应元素的迭代器,若无对应元素,则返回指向end()。
erase(iterator); 删除迭代器指向的元素;
insert(T val); 插入元素
若T为结构体,则需重载 < 运算符
map
优先队列(priority_queue)
特殊队列。每次从队列中取出的是具有最高优先权的元素。\
自定义优先级:
重载运算符
1
2
3
4
5
6
7//小优先
struct cmp
{
bool operator () (T a, T b)
return a.val > b.val;
}
priority_queue<T, vector<T>, cmp> pq;
其他
智能指针(shared_ptr)
- ss
字典序
C++
- static的用法
- 静态局部变量
- 静态全局变量
- 静态函数