链表
链表反转:
开始先设定三个指针,并进行初始化,如图
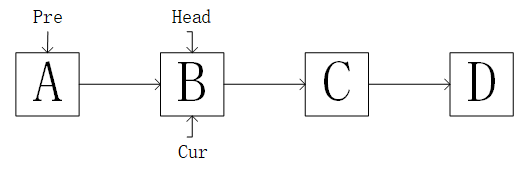
并将Pre的指向的Next指向NULL
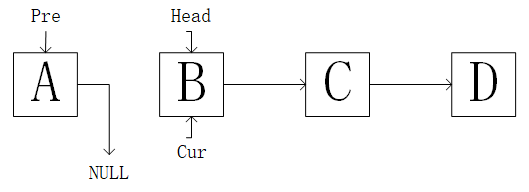
开始循环,head指针后移,让Cur指针的Next指向Pre,然后使Pre = Cur,Cur = Head。直到链表尾
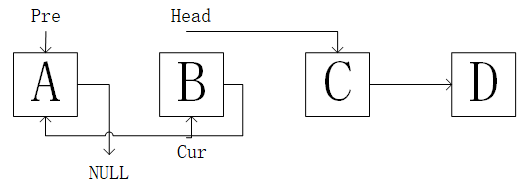
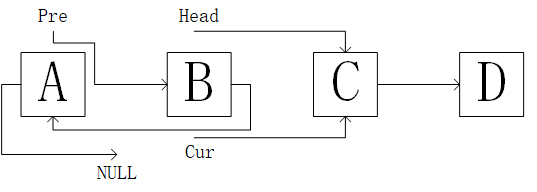
二分法模板:
1
2
3
4
5
6
7
8
9
10
11
12
13int l = 0, r = nums.size() - 1;
int mid = 0;
while (l <= r) {
mid = l + r >> 1;
if ("根据题目判断搜索条件") {
l = mid + 1;
}
else {
r = mid - 1;
}
}
return l;
广度优先遍历(BFS)
1
2
3
4
5
6
7
8
9
10
11
12
13
14void levelOrder(TreeNode* root) {
queue<TreeNode*> qu;
if(root)
qu.push(root);
while (!qu.empty()) {
TreeNode* t = qu.front();
qu.pop();
cout << t->val;
if(t->left)
qu.push(t->left);
if(t->right)
qu.push(t->right);
}
}
深度优先遍历(DFS)
- 例题:剑指 Offer 12. 矩阵中的路径
- 用dfs深度遍历加回溯法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37bool exist(vector<vector<char>>& board, string word) {
if (board.empty() || board[0].empty())
return false;
//循环查找,每个字符都可能是第一位
for (size_t i = 0; i < board.size(); i++)
{
for (size_t j = 0; j < board[0].size(); j++)
{
if(dfs(board, word, i, j, 0)) return true;
}
}
return false;
}
bool dfs(vector<vector<char>>& board, const string& word,
int row, int col, int idx) {
if (idx == word.length()) {
return true;
}
if (row < 0 || row >= board.size() ||
col < 0 || col >= board[0].size() ||
board[row][col] != word[idx]) {
return false;
}
//将遍历过的,和word字符匹配的位置置为不可能出现的字符,起到visited数组的作用
board[row][col] = '\0';
//进行递归遍历
if (dfs(board, word, row - 1, col, idx + 1) ||
dfs(board, word, row + 1, col, idx + 1) ||
dfs(board, word, row, col - 1, idx + 1) ||
dfs(board, word, row, col + 1, idx + 1))
return true;
//若此次遍历无匹配,则将数组字符还原
board[row][col] = word[idx];
return false;
}
字符串
清除字符串前后的空格符号
1
2
3
4
5if (!s.empty())
{
s.erase(0, s.find_first_not_of(" "));
s.erase(s.find_last_not_of(" ") + 1);
}
二叉树
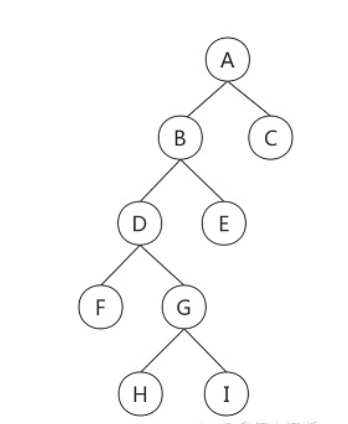
前序遍历:优先遍历根节点,然后是左子节点,再是右子节点
A-B-D-F-G-H-I-E-C
中序遍历:优先遍历左子节点,然后是根节点,再是右子节点
F-D-H-G-I-B-E-A-C
后序遍历:优先遍历左子节点,然后是右子节点,再是根节点
F-H-I-G-D-E-B-C-A
二叉树转化成双向链表:
用中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28//head保存双向链表头节点,pre保存中序遍历时的前一个遍历的节点
Node* pre = NULL, * head = NULL;
Node* treeToDoublyList(Node* root) {
if (!root) return NULL;
dfsm(root);
//使首尾相连
head->left = pre;
pre->right = head;
//返回头节点
return head;
}
void dfsm(Node* root) {
if (!root) {
return;
}
dfsm(root->left);
//如果pre为空,则此节点为第一个节点,所以记录下头节点
if (!pre)
head = root;
//不为空则表示已经遍历过其他节点,因此使上一个节点指向此节点
else if (pre)
pre->right = root;
//双向链表,因此此节点的左指针指向上一个节点
root->left = pre;
pre = root;
dfsm(root->right);
}
数据结构
优先队列:priority_queue
包含在头文件 ‘queue’ 中,我们可以自定义其中数据的优先级, 让优先级高的排在队列前面,优先出队.
优先队列具有队列的所有特性,包括队列的基本操作,只是在这基础上添加了内部的一个排序,它本质是一个堆实现的
1
2
3
4
5//升序队列,小顶堆
priority_queue <int,vector<int>,greater<int> > q;
//降序队列,大顶堆
priority_queue <int,vector<int>,less<int> >q;
二叉搜索树:Binary Search Tree
算法
相同数字异或为零
1 | class Solution { |
